Optimization is one of the most studied areas in the wide field of artificial intelligence. Hundreds of studies are published year after year focused on solving many diverse problems of this kind. In a nutshell, an optimization problem can be defined as the intelligent search of the best solution from the whole group of feasible ones. The specific word best refers in this context to the most desired solution related to any objective function (or fitness function), which is expected to be maximized or minimized. In other words, an optimization procedure consists of finding the optimal solution to a problem taking into account i) the previously mentioned objective function, which provides a quantitative measure of the performance ii) the decision variables that compose the optimization problem and the parameters on which the solving algorithm is based on, and iii) the constraints to be compulsorily met which delimits the allowable search space.

Efficiently tackling such optimization problems requires huge computational resources, especially when the formulated problem at hand represents complex real-world situations with hundreds of variables and constraints. For these reasons, and due to the inherently practical utility of optimization algorithms, very heterogeneous problem-solving approaches have been developed by the community over the last decades for their application to these problems.

In the specific context of PIACERE, optimization represents one of the crucial aspects for the proper working of the whole system. More specifically, this optimization will be the cornerstone of the component known as IaC Optimized Platform(IOP). Briefly described, the IOP is responsible for finding the best possible set of infrastructural elements given the input data received. This input data provided will include i) the optimization requirements, i.e: establish a maximum cost for the whole system, fix a minimum required expected performance, or a minimum expected availability; ii) Optimization requirements, that is, the objectives to optimize, such as the minimization of the cost and the maximization of the availability, iii) and the infrastructure model . Then, the IOP will use an advanced optimization algorithm, seeking for an optimized deployment configuration of the IaC on the appropriate infrastructural elements that best meet the predefined constraints. The IOP will success if it is able to propose the most optimized deployment configuration of the infrastructural code taking into consideration the constraints predefined.

In order to properly understand the problem modelled in the context of PIACERE, we introduce now a simplified example using a reduced catalogue of infrastructural elements. For doing this, please, consider a simplified use case in which the user needs to deploy an application needing just three different elements:

[Virtual Machine, Database, Storage]

Furthermore, we assume for each of these elements, five different options are available:

• Virtual Machine: [A3_France, A2_USA, B8_Germany, C1_Spain, c2_Europe]
• Database: [dynamo.4, m3.medium, mysql.AZ_1, postgreSQL.G, r4.4xlarge]
• Storage: [Standard_Europe, Standard_USA, Storage3_Spain, G_1, AZ_3]

Each of these elements has some associated attributes such as cost, expected performance, availability, region, provider, type or capacity. With all this, the main optimization problem is to find the best combination of [Virtual Machine, Database, Storage] which optimizes a certain objective or some defined objectives.

In this specific example, and in the context of PIACERE, the problem is defined as a multi-objective one, seeking to optimize two or more different opposite objectives. In this example we deem the optimization of two different objectives: cost and availability.

In order to find this best solution, the solving algorithms developed in PIACERE should assign a numeric value to each option of every element. For example, the Virtual Machine element can vary within this set of values {0:“A3_France”, 1:”A2_USA”, 2:”B8_Germany”, 3:”C1_Spain”, 4:“C2_Europe”}. This way, an algorithm can define a tentative solution with this form:

[0, 3, 1]: [295.5, 125.2]

Meaning that the tentative solution for the [Virtual Machine, Database, Storage] combination is [A3_France, postgreSQL.G, Standard_USA]. Furthermore, this solution has both a cost and an availability value associated, which is the second array [295.5, 125.2]. This means that the cost associated to this solution is 125.2 while the availability is 295.5.

Furthermore, being a multi-objective optimization problem, the resolution of a problem of this kind entails the finding of a group of solutions which provide the optimal balance among the considered objectives, in this case the cost and the availability. In this kind of optimization, one solution can be deemed as Pareto optimal whether there is no other solution better than it in all considered objectives. This is the main reason why the solving objectives should be mutually competitive. Thus, the solution of the problem introduced in this post is a group of solutions as the one depicted in the following figure, which is composed by 9 different solutions. These solutions optimally balance the objectives considered in the problem at hand, leaving the final decision of choosing one in hands of an external decision engine or in the criterion of the final user.

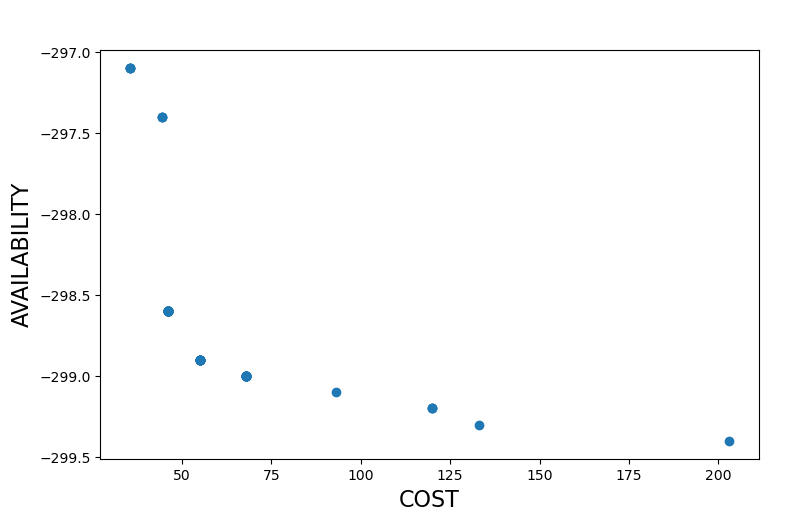
Figure 1: Pareto-front including best solutions to the introduced multi-objective optimization problem.

As a conclusion, the efficient modelling of the optimization problem is one of the most crucial and critical aspects in any project. Having met this first cornerstone, the next steps in PIACERE are the efficient developing of metaheuristics optimization techniques, able to provide good solutions to the user for any kind of environments. Some important steps have been conducted already in this context, so stay tuned to PIACERE BLOG in order to receive more interesting information about this progress!